| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 데이터베이스시스템
- 직선의방정식
- 2023채용박람회
- 정보처리기사공부방법
- wxmaxima
- 아이엔이야기
- 다자녀장학금
- 숫타니파아타
- 청년도배사 이야기
- kgol
- 이분그래프
- 오일러투어
- 무소의뿔
- 티스토리챌린지
- 윤파고
- 오블완
- 허스켈그래프
- 이런 사람에게 "절대" 돈과 시간 쓰지 마세요. (이헌주 교수 3부)
- 최단경로문제
- 맥북에서 wxMaxima 설치
- playground배열
- 나르시스트
- 배윤슬
- 그래프2
- 집착형
- 등록금0원
- wxMaxima install for mac os
- 쌍대성원리
- 합의정리
- 제거된값 첨부하기
- Today
- Total
사적공간
정수의 분류 문제 본문

정수의 성질을 이용한 문제다.
예제의 풀이를 참고하여 문제를 풀었으며, 풀이내용이 석연치 않다.
문제에서
1)3으로 나눈 나머지가 1인 수는 = 3m+1
2)5로 나눈 나머지가 3인 수는 = 5n+1
3) 100이하 자연수 (0<x<=100)
3m+1만 수열로 나타내면
차이
| 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | ... |
조건을 만족하는 숫자
1 4(1+3n) 7 10 ...
n=0 n=1 n=2 n=3
0~1: 차이 1
1~3: 차이 2
그 다음부터는 차이 3...
1)3으로 나눈 나머지가 1인 수는 = 3m+1
2)5로 나눈 나머지가 3인 수는 = 5n+3
3) 100이하 자연수 (0<x<=100)
3가지 조건을 만족해야 한다.
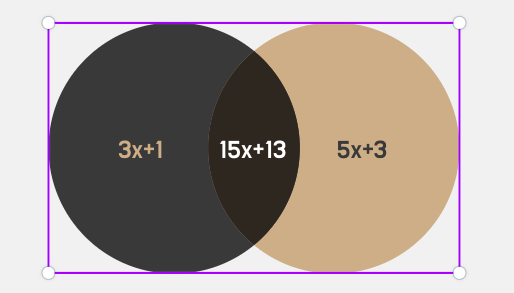
1)와 2)가 이고(곱셈법칙?)으로 연결되어 있으므로 해당문제는 집합으로 표현하면 교집합으로 나타낼 수 있다.
3)을 추가해서 1)과 2)와 3)의 교집합을 구하는 문제다.
풀이순서
1)과 2)의 교집합을 구한다.
1)과 2)를 동시에 만족하는 수를 구해야 하는데, 1)에 속하는 수 중에서 2)를 만족하는 수를 구해야 한다. 2) 중에는 1)을 만족하지 않는 수도 있다.
공식 : kn+-(k-1)
n은 정수
5n+0
1)과 2)의 교집합의 수
= 3(5n+3)+1
= 15n+10
= 5로 묶으면 5(3n+2) -> 조건 불만족
= 3(5n+4)+1
= 15n+13
= 5로 묶으면 5(3n+2)+3 -> 조건 만족
반대로
5(3m)+3
= 15m+3
= 3(5m+1)+0 조건 불만족
5(3m+1)+3
= 15m+8
= 3(5m+2)+2 조건 불만족
5(3m+2)+3
= 15m+13
= 3(5m+4)+1 조건 만족
-> 15m+13
15m+13 이면서 100이하의 자연수는
1] m=0, 13
2] m=5, 75+13 = 88,
m=6, 90+13 = 103 초과됨 x
1] + 2] = 답: 6개
1)3으로 나눈 나머지가 1인 수는 = 3m+1
2)5로 나눈 나머지가 3인 수는 = 5n+3
3) 100이하 자연수 (0<x<=100)
의문점
여기서 조건이란 3으로 나누어서 1이 남고, 5로 나누어서 3이 남게 되는 동치를 말함.
위 식 3m+1에서 m에 5n+0..1..2..3..4... 을 차례로 대입해보는 건
이미 3m+1로 1)의 조건은 만족했고, 2)의 조건을 만족하는 식을 찾기 위함임.
1)로 구분된 수 중에서 2)로 구분된 수를 찾는데,
1>> 1) 식에 2)식을 바로 대입하지 않는지,
2>> 왜 대입한다는 발상이 가능한건지,
3>> 많은 수중에서 5로 나눈 나머지 식들을 무차별로 대입해서 조건을 확인해봐야 하는지 명확하지 않다.
누군가 문제에 대해 명쾌한 설명이 가능하다면 댓글을 달아주길 바란다.
다시 정리하면
? = 3(5로 나눈 나머지에 의해 분류 중 하나의 규칙)+ 1 = 3으로 나누어서 1이 남는 수 <-> 5로 나누어서 3이 남는 수
| 1 | 3 | 3 | 3 | 3 | 3 | |
| 3 | 5 | 5 | 5 | 5 | 5 |
n: 1 2 3 4 5 6 7 8 9 ...13....
3n+1: 1 4 7 10 13 ...
5n: 0 5 10 15 20 25 30
5n+1: 1 6 11 16 21 ...
5n+2: 2 7 12 17
5n+3: 3 8 13 18 5씩 건너뛰긴 하지만 시작점이 다르므로 찍히는 숫자도 다름.
5n+4: 4 9 14 19 24 29 ...
15m+13: 13 28 43...
'수학' 카테고리의 다른 글
| 수학올림피아드/ MAT수학시험/ 대학편입 수리논술/바칼로레아/ 인문학시험 (재미있을 듯 ) (0) | 2025.03.19 |
|---|---|
| 배워서 남준다 (0) | 2025.02.12 |
| 삼각함수 그래프 (0) | 2022.08.24 |
| 좌표평면에서 직사각형의 넓이를 이등분 하면서 원점을 지나는 직선의 방정식 구하기 (0) | 2022.08.19 |

