| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- wxMaxima install for mac os
- 숫타니파아타
- playground배열
- 2023채용박람회
- 집착형
- 맥북에서 wxMaxima 설치
- 그래프2
- 오블완
- 아이엔이야기
- 정보처리기사공부방법
- 최단경로문제
- 이분그래프
- 쌍대성원리
- 이런 사람에게 "절대" 돈과 시간 쓰지 마세요. (이헌주 교수 3부)
- 오일러투어
- 나르시스트
- 윤파고
- 티스토리챌린지
- 배윤슬
- kgol
- 직선의방정식
- 무소의뿔
- 제거된값 첨부하기
- 다자녀장학금
- 허스켈그래프
- 데이터베이스시스템
- wxmaxima
- 등록금0원
- 합의정리
- 청년도배사 이야기
- Today
- Total
사적공간
그래프1 차수에 관해 생각해보기 본문
동기
cf) 동일한 개념에 대해 강의안에만 있거나 교재에만 있는 내용(깊이)이 존재함. U - (A ∩ B) 가 있는 a∈A 혹은 b∈B 가 존재
아래 내용은 그 중 하나
이산수학 강의안 제 9장 그래프(1) p19 노란박스에
참고: 그래프에서 '차수가 홀수인 꼭지점의 수'는 짝수이다. 가 잘 안 와닿아서 나름 생각해봄.
기본개념
G = (V,E) v는 V의 원소
차수(degree) = [deg(v)] = v에 인접한 변의 개수
총차수(total degree) = [deg(G)] = G에 속한 모든 꼭지점의 차수의 합
deg(v) = 2|E|
생각해보기
그래프를 차수가 홀수인지 짝수인지로 구분했을 때, 3경우 나뉨
1) 차수가 모두 짝수인 꼭지점만 있는 그래프
2)차수가 모두 홀수인 꼭지점만 있는 그래프
3) 차수가 홀수와 짝수가 섞여있는 그래프
아래문장은 위 3경우에 모두 해당됨.
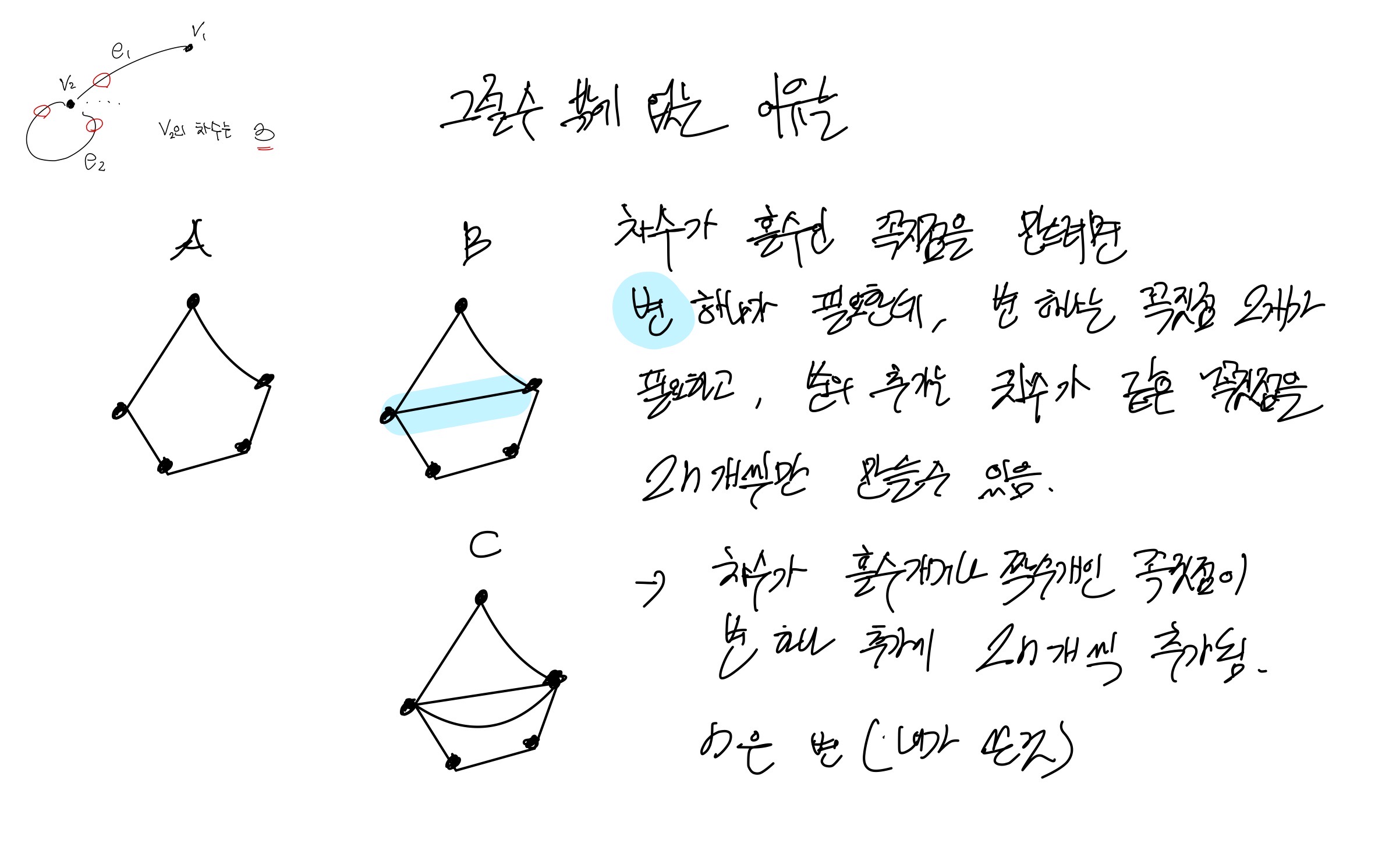
그래프에서 '차수가 홀수인 꼭지점의 수'는 짝수있다.
변 하나에 꼭지점 두 개가 발생되는 한, 그래프 전체의 차수는 항상 짝수만 나올 수 밖에 없고, 공식 deg(v)= 2|E| 가 가능해짐.
(꼭지점 하나에 루프가 하나 있을 경우, 그 그래프는 변 하나에 꼭지점이 두 개가 발생하진 않지만, 꼭짓점 입장에선 차수가 2n개씩 추가되는 것임.


이렇게 공식? 을 일리있게 풀어 써봐도 막상 공식을 사용할 때는 맹목적으로 원리를 생각하지 않고 사용하게 되는게 문제임.
논리적으로 정리가 안돼서 직관적으로 이해하지 못하는 것 같기도 함.
참고: 방송통신대학교 이산수학과 이산수학 강의안
'KNOU_CS > 이산수학' 카테고리의 다른 글
| 트리-교재 앞부분 용어정리&공식 생각해보기(보충 및 정리 필요) (0) | 2022.08.17 |
|---|---|
| 그래프2- 오일러 투어&최단경로문제 알고리즘 (0) | 2022.08.11 |
| 그래프1 이분그래프 (0) | 2022.08.09 |
| 부울대수 (0) | 2022.08.09 |
| 이산수학 학습주안점 (0) | 2022.08.02 |




